The first time I heard of the term "color space" was probably from some article about display color gamut/calibration. I learned that it is important for a display to achieve at least 100% sRGB, for digital painting or image processing. Well I didn't know what exactly "s" means here, but I got a feeling that it has something to do with the RGB values in HTML color codes.
The diagram could be very confusing. I had a few questions, which I think I can answer today:
Why does it look like a weird 2d shape, instead of a 3d volume?
It is a 2d shape, which is a slice of the 3d space at a constant luminance.
More specifically, this is a sliced xy space at a specific value of Y.
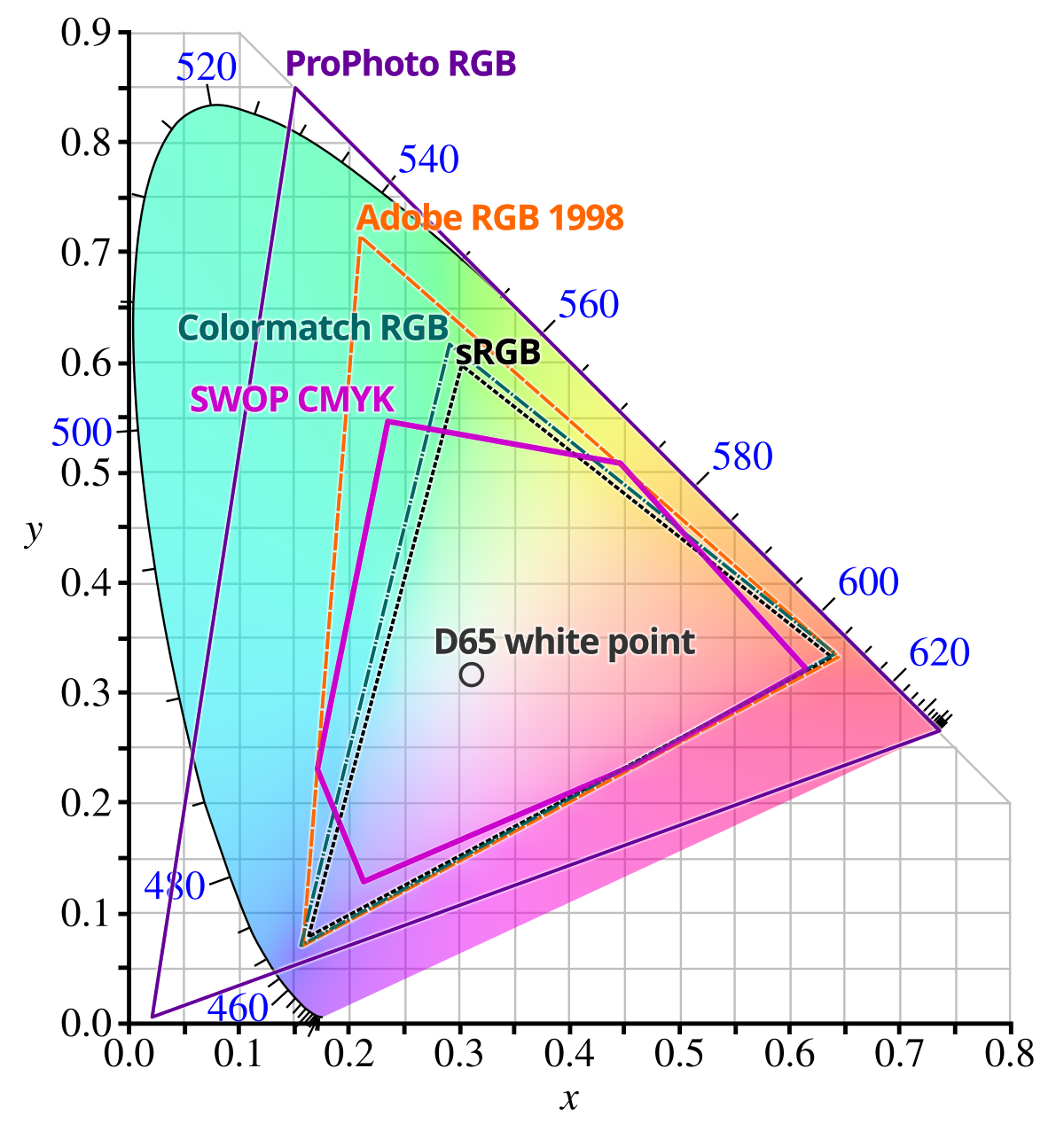
Why does the sRGB color space appear as a triangle?
The sRGB color space is generated by 3 primary colors, which corresponds to the 3 vertices of the triangle. Moreover, for any 2 colors, all available colors obtained by mixing these 2 colors (with different ratios) corresponds to all points on the line segment that connects the 2 points.
Assuming RGB values, (1, 1, 0) may be obtained by mixing (1, 0, 0) and (0, 1, 0). However they are not on a line.
The idea is that luminance and chromaticity may be examined independently. (1, 1, 0) would have the same chromaticity as (0.5, 0.5, 0), which is on the line segment connecting (1, 0, 0) and (0, 1, 0).
However, note that (0.5, 0.5, 0) is not necessarily the middle point on the xy diagram. Simliarly, the white point is not necessarily the gravicity center of the triangle.
This wiki page lists and compares a number of color spaces. Here are my notes:
CAM - Color Appearance Model, which describes human perceiption of colors. These models could be useful for choosing colors. Difficult to compute. Examples: CAM16, Oklab, CIECAM02, CIELAB.
UCS - Uniform Color Space, in which the distance between two color points reflects the color difference perceived by human. These models could be useful for generating gradients. Difficult to compute. Examples: CAM16-UCS, OSA-UCS.
RGB - Generated with 3 primary colors. It is widely used for display devices and media encoding. The linear version (without gamma correction/encoding) is also useful for mixing colors (lights) and rendering. Easy to compute. Examples: sRGB, Adobe RGB.
HSV, HSL, HSI, HSY - Cylindrical transformations of RGB. Widely used for historical reasons. Easy to compuate but very inaccurate.
Finally, I found the following videos very helpful:
Comments